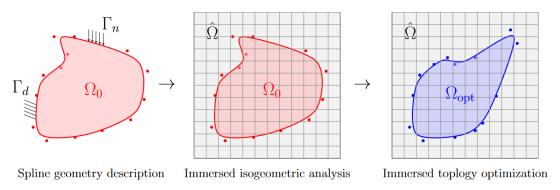
Topology optimization is a powerful tool for designing complex structures with optimal mechanical properties. It is widely used in engineering applications, such as aerospace, automotive, and civil engineering. Isogeometric analysis (IGA) is a relatively new numerical method that integrates computer-aided design and finite element analysis using the same basis functions, resulting in more accurate and efficient simulations. On the other hand, immersed boundary methods (IBM) have been developed to avoid the difficulty of meshing complex domains. In this regard, immersed boundary conformal isogeometric analysis (IBC-IGA) combines the efficacy of IBM with the accuracy of IGA by using immersed discretizations with boundary-conformal quadrature rules.

The aim of this thesis is to develop a novel approach for topology optimization of linear elasticity problems in solid mechanics using immersed boundary conformal isogeometric analysis (IBC-IGA). In particular, the explicit description of the boundaries of the optimal topology as spline curves shall be combined with the boundary-conformal quadrature method. In this way, it will be possible to represent complex geometries with relatively few design variables and facilitate efficient gradient-based design optimization.